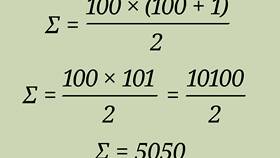Сумма последовательных чисел - это результат сложения ряда целых чисел, идущих друг за другом в порядке возрастания или убывания. Это фундаментальное понятие в математике имеет широкое применение в различных вычислениях.
Содержание
Основные понятия
Последовательные числа - это числа, которые следуют одно за другим с постоянным шагом. Чаще всего рассматриваются:
- Последовательные натуральные числа (1, 2, 3, ...)
- Последовательные четные числа (2, 4, 6, ...)
- Последовательные нечетные числа (1, 3, 5, ...)
- Последовательные целые числа с произвольным шагом
Формулы для вычисления суммы
| Тип последовательности | Формула суммы |
| Натуральные числа от 1 до n | S = n(n+1)/2 |
| Четные числа от 2 до 2n | S = n(n+1) |
| Нечетные числа от 1 до (2n-1) | S = n² |
Примеры вычислений
Рассмотрим конкретные примеры сумм последовательных чисел:
- Сумма чисел от 1 до 10: 1+2+3+...+10 = 55
- Сумма четных чисел от 2 до 10: 2+4+6+8+10 = 30
- Сумма нечетных чисел от 1 до 9: 1+3+5+7+9 = 25
Историческая справка
Известная легенда связывает понятие суммы последовательных чисел с именем Карла Гаусса:
- В детстве Гауссу предложили сложить числа от 1 до 100
- Он заметил, что можно парно складывать первое и последнее число
- 1+100 = 101, 2+99 = 101, и так далее
- Получилось 50 пар по 101, итого 5050
Практическое применение
Суммы последовательных чисел используются в:
- Финансовых расчетах (аннуитеты, кредиты)
- Компьютерных алгоритмах
- Теории вероятностей
- Физических вычислениях
Обобщенная формула
Для любой арифметической прогрессии a₁, a₂, ..., aₙ сумма вычисляется по формуле:
| S = n(a₁ + aₙ)/2 | где n - количество членов |
Сумма последовательных чисел - это важное математическое понятие, которое находит применение во многих областях науки и практической деятельности.